Циклическое выполнение команд в зависимости от свойств данных

О соотнесении рекурсии и цикла: как правило необходимости в дополнительных пространствах имён нет, достаточно просто повторять одну и ту же последовательность действий, пока не изменятся свойства обрабатываемых данных.

Цикл

• Цикл while

  • Цикл со счётчиком

       1 n = 0           # инициализация
       2 while n<10:     # проверка условия
       3     print(n)    # тело
       4     n += 1      # изменение данных, участвующих в условии
    

  • Пошаговый просмотр

  • Цикл с непредсказуемым окончанием (например, ввод до 0)

    n = int(input())      # инициализация
    while n:              # проверка условия
        print(n*2+1)      # тело
        n = int(input())  # изменение данных, участвующих в условии
    print("Done")

  • Бесконечный цикл

       1 n = 0
       2 while n<10:
       3     print(n)
       4     # n += 1
    

• ⇒ Каноническая схема цикла
  1. инициализация
  2. проверка условия
  3. тело
  4. изменение
• Вложенные циклы

     1 N = 4
     2 i = 1
     3 while i<=N:
     4     j = 1
     5     while j<=N:
     6         print(i, "*", j, "==", i*j)
     7         j += 1
     8     i += 1
  

  • Пошаговый просмотр

  • Место инициализации во вложенном цикле.
    • Вот этот код работает неправильно, потому что инициализация внутреннего цикла не находится непосредственно перед запуском этого цикла (⇒ выполняется всего один раз в самом начале)

         1 N = 4
         2 i = j = 1
         3 while i<=N:
         4     while j<=N:
         5         print(i, "*", j, "==", i*j)
         6         j += 1
         7     i += 1
      

TODO

• Условные операторы в цикле

• Операторы break и continue, когда нужны

• Алгоритм «поиск первого», секция else: в цикле

Немного про форматные строки

• Понятие о подстановке в шаблон

• Форматная срока: f"произвольный текст{выражение:правила форматирования}произвольный текст…"

  • Фигурные скобки — это шаблон, выражение в них вычисляется и в строку подставляется результат

    •    1 a, b = 4, 5
         2 print(f"---===< {a}*{b}=={a*b} >===---")
      

  • После ':' в шаблоне указывается, как форматировать. Число означает ширину в символах. Если оно слишком большое, оставшееся место заполнится пробелами. Если оно слишком маленькое, подставится нужное количество символов, и форматирование «поедет».

    •    1 print(f"{a:7}**{b:5}=={a**b:2}")
      

  • Можно указать, к какому краю отведённого места прижимать подстановку шаблона. '<' — к левому, '>' — к правому (по умолчанию), '^' — к середине

    •    1 print(f"{a:^7}*{b:<7}=={a*b:6}")
      

  • Числа могут быть дополнены незначащими нулями. У вещественных чисел указывается общая ширина

    •    1    a,b=2225,6
         2    f"{a:03}/{b:03}=={a/b:15.10}"
      

• Язык форматирования

Д/З

0. Прочитать и прощёлкать седьмую главу учебника

1. Вводить целые числа до тех пор, пока среди них не встретится 0, и посчитать, сколько среди них было кратных трём (0 не считается). Вывести это значение.

   • Ввод:

    1
    2
    3
    4
    3
    7
    9
    3
    7
    0

   • Вывод:

    4

2. Ввести натуральное число N и проверить, является ли оно точным кубом некоторого натурального числа. Сравнивать вещественные числа (то есть проверять, содержит ли n**(1/3) ненулевую дробную часть) запрещено.

   • Алгоритм: для всех чисел i от 1 проверять, не равно ли i**3 == N, заканчивать цикл, когда i**3 больше N
3. Ввести натуральное N и вывести все простые числа, не превосходящие N (простыми называются числа, которые делятся только на себя и на 1)
   • Алгоритм:

       для всех i от 2 до N (1 — не считается простым)
           для всех k от 3 до i-1 (на самом деле до корня из i, ну да ладно)
               если i делится на k, оно не простое, можно больше не проверять
           если i ни на какое k не делится, оно простое, вывести

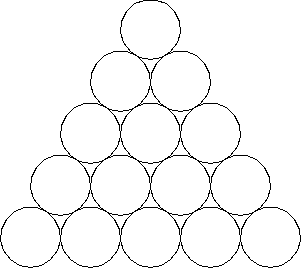
4. Ввести два натуральных числа, N и R и нарисовать пирамидку из N слоёв окружностей радиуса R (можно воспользоваться функцией turtle.circle(радиус)). Вершина пирамиды содержит одну окружность, второй слой — две и т. д.

   • Ввод:

       5,30

     Вывод